上篇文章中,我们实现了神经网络各层的误差反向传播版本,现在我们把之前用数值微分实现的手写数字识别改进一下,用误差反向传播来实现。老规矩,完整代码在文末。
两层神经网络
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size,
weight_init_std=0.01):
# 初始化权重
self.params = {}
self.params['W1'] = weight_init_std * \
np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * \
np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
# 生成层
self.layers = OrderedDict()
self.layers['Affine1'] = \
Affine(self.params['W1'], self.params['b1'])
self.layers['Relu1'] = Relu()
self.layers['Affine2'] = \
Affine(self.params['W2'], self.params['b2'])
self.lastLayer = SoftmaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
# x:输入数据, t:监督数据
def loss(self, x, t):
y = self.predict(x)
return self.lastLayer.forward(y, t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
if t.ndim != 1:
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.lastLayer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 设定
grads = {}
grads['W1'] = self.layers['Affine1'].dW
grads['b1'] = self.layers['Affine1'].db
grads['W2'] = self.layers['Affine2'].dW
grads['b2'] = self.layers['Affine2'].db
return grads对比上次数值微分的实现,在初始化函数__init__()中,我们用一个有序字保存了各层,以便于稍后按顺序进行正向、反向传播。在predict()函数中,我们直接调用各层的forward()进行正向传播,最大的不同就在于gradient()的函数,它是使用反向传播实现,比之前使用数值微分实现的效率要高得多。
因为反向传播的高性能,所以很快就可以完成人工智障的训练,我们把训练过程的损失函数值、测试精度绘制出来,可以看到损失函数在不断下降,下降的速度不断变慢,最后趋于平稳,精度不断提高,最后也趋于平稳,如下: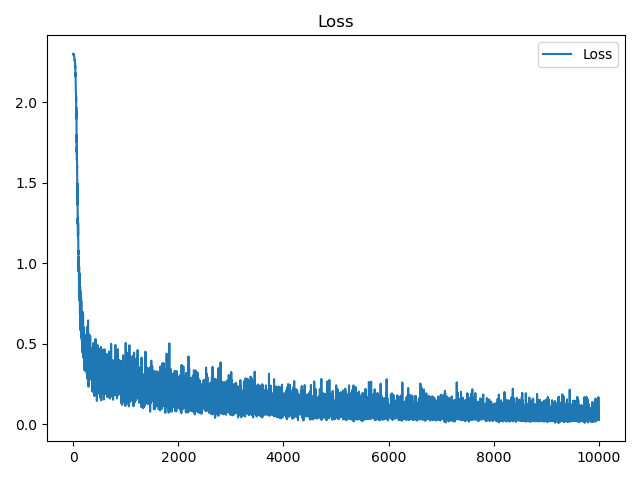
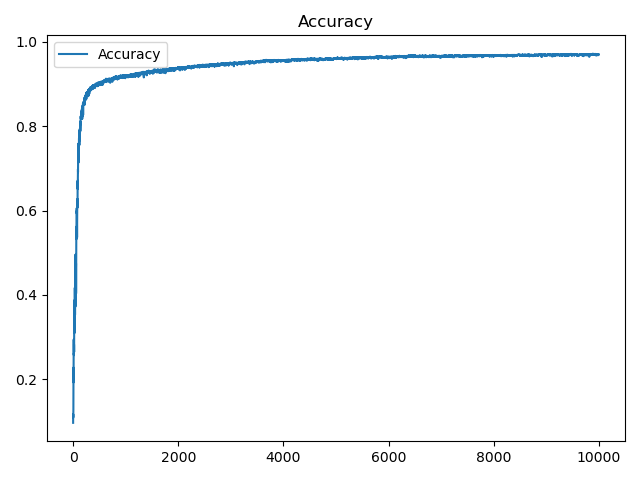
接下来随机从测试集中选取一个图片用人工智障识别测试一下: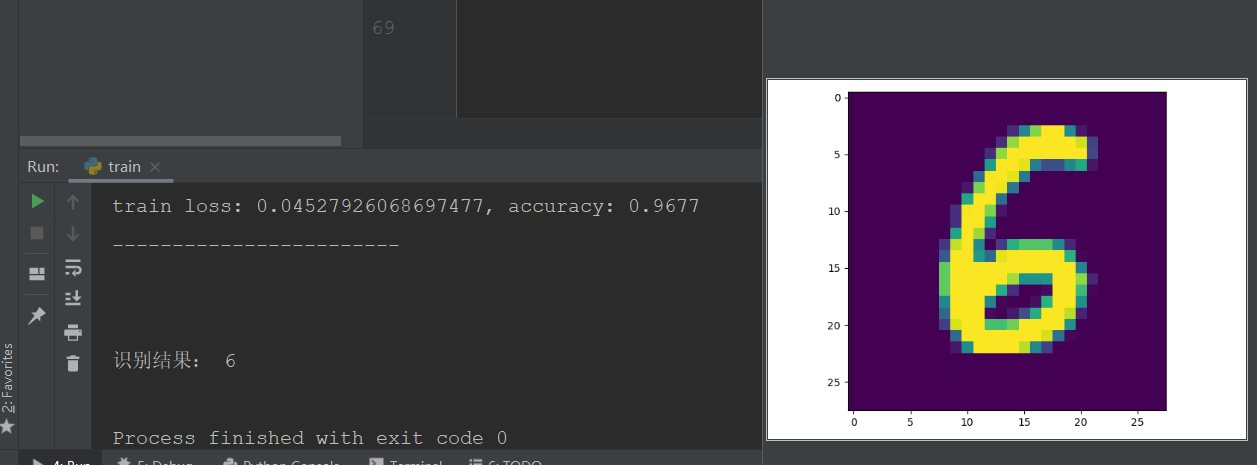
可以看到,人工智障正确识别了图片中的数字。我训练10000轮后精度约为0.9677,还是比较高的,但和使用卷积神经网络这些相比,这一精度并不高,后面我们慢慢改进,将这一模型各项指标(查准率、召回率、泛化能力等)提高。
完整代码:点击下载

Comments | NOTHING